[Accueil du site. ] _ [Lycée] _ [GAFAM et comment y échapper.] _ [Sur Gnumeric]

Un problème avec Gnumeric

1°) Ce que l'on veut faire.

1°_a) Principe

Il s'agit de réaliser des calculs de statistiques de niveau terminale.
Gnumeric a été choisi à cause de sa réputation d'être particulièrement adapté à ce domaine.

Sur un tableau de n=38 valeurs, générées aléatoirement, on veut apprendre à calculer les grandeurs habituelles.

• Moyenne des valeurs du tableau.
• Variance
• Écart type.
• Incertitude type.

Ces calculs seront fait en utilisant les fonctions intégrées de Gnumeric, d'une part, et par un calcul détaillé utilisant les possibilités des tableurs et les formules de définition des grandeurs, d'autre part.

1°_b) Calcul de la moyenne

Ce calcul n'offre pas de difficulté.

On utilise d'une part la fonction :
=average(valeur1 : valeur38),
d'autre part avec la fonction
=sum(valeur1 : valeur38)
la formule bien connue : Moyenne = (somme des valeurs)/(n). avec ici n=38.

N.B.0 : le séparateur pour indiquer l'ensemble des valeurs de la première à la dernière est comme souvent, le double point :.

N.B.1 : j'ai essayé d'utiliser MathML, mais cela ne fonctionne pas dans les navigateurs Falkon et lynx.
Je craignait donc que cela soit moins accéssible pour les mal-voyants et les gnous furieux.

Essai avec MathML, qui ne fonctionne bien que dans Firefox :

À l'avenir je vais tenter d'utiliser la bibliothèque MinMathJS écrite par Eric Leydet:
http://progmath.free.fr/minmathjs/index.html
http://eleydet.free.fr/mmjs_formule.zip

1°_c) Calcul de la variance

Là aussi, 2 calculs,
d'une part la fonction intégrée :
=var(valeur1 : valeur38),
d'autre par l'application pas-à-pas de la définition, à savoir : la moyenne des carrés des écarts à la moyenne (wikipedia)
Pour cela un calcul pas à pas, par colonnes à été effectué.

1°_d) Calcul de l'écart type

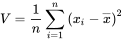
On utilisera d'une part la fonction :
=stdev(valeur1 : valeur38)
d'autre part simplement la racine carrée de la variance préalablement calculée.

2°) Les tableaux de valeurs

2°_a) Les valeurs initiales

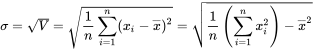
Tout d'abord, une première colonne avec la valeur de l'indice i est générée très basiquement par un copié collé verticale de la formule
[=i+1]
de haut en bas, la première case étant remplie par la valeur 1.
Cette première colonne ne sert pas vraiment dans les calculs.

La seconde colonne, avec les valeurs de x_i est générée par la fonction de production de valeurs pseudo aléatoires rand() (sans argument) de gnumeric.
= rand()*2 + 1
On devine que la moyenne sera proche de 2.

2°_b) Les valeurs intermédiaires

Dans une colonne voisine on calcule l'écart à la moyenne pour chaque ligne, donc pour chaque valeur de x_i
puis dans une quatrième colonne on calcule le carré de la valeur précédente avec la fonction :
= power(x_i,2).

Oui. Nous avançons prudement, étape par étape.

Cela donne ce tableau.

3°) Résultats des calculs

C'est là qu'apparait une bizarerie subtile.

3°_a) À la main à l'ancienne (comme la baguette de pain bio)

Le calcul à la main à partir des formules donne :

N.B.2 : On retrouve les mêmes valeurs en exploitant la fonction average (moyenne).

Puis pour obtenir l'écart type, il suffit de faire la racine carrée de la variance.
=sqrt(variance), ce qui donne σ= 0,5698588012670364.

3°_b) les résultats des fonctions intégrées

Mais l'utilisation des fonctions
=var(valeur1 : valeur38) (variance) et
=stdev(valeur1 : valeur38) (écart type), ne donne pas les mêmes résultats !

Par ces fonctions directes on a :

Ce sont des valeurs légèrement supérieures, donc résultats d'une division par un dénominateur inférieur à 38.
Une vérification rapide permet de constater que pour les fonctions intégrées, le dénominateur utilisé est 37, soit n-1 dans les formules.

En passant par le menu [Statistiques]
puis [Statistiques descriptives],
et de nouveau [Statistiques descriptives],
on dévoile une fenètre qui déclenche le calcul de l'ensemble des grandeurs statistiques communément demandées.

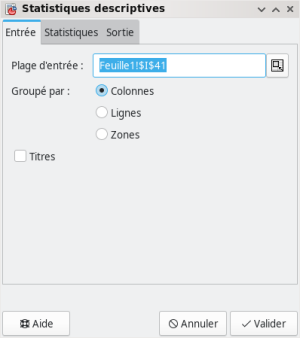
On retrouve les valeurs des fonctions var et stdev en 1/(n-1).

N.B.3 : Les fonction correspondantes de LibreOffice Calc var et ecartype donnent les mêmes résultats en 1/(n-1).

N.B.4 : Un peu de recherche dans certains livres de physique de préparation au bac donne effectivement des formules d'écart type sur (n-1) au lieu de n sans qu'aucune explication ne soit donnée.

3°_c) un bout d'explication

Après enquête, il s'avère que les formules de variance et écart type en 1/n correspondent à l'analyse d'un tableau d'une population complète de valeurs, ce qui est bien dans un exercice de mathématique de lycée,
tandis que les formules en 1/(n-1) correspondent à l'étude d'un échantillonage de valeurs prélevées sur une population, ou un phénomène, donc par nature un tableau incomplet.

Des mathématiciens plus compétents que l'auteur de cette page en on décidé ainsi. Ils devaient avoir de bonnes raisons pour cela, que nous ne contesterons pas.

L'un d'entre eux fait quelques remarques : ici

4°) Un bout de solution

Dans le tableur gnumeric, sur une population complète, il faut donc utiliser en lieu et place de var et stdev, les fonctions
varp et stdevp
dont le p final signifie bien qu'elles s'appliquent à des populations.

Liste des fonctions de gnumeric évoquées

Génération de nombres aléatoires

=rand()
sans argument.

Somme des valeurs d'un tableau

=sum(valeur₁ : valeur_n)

Moyenne des valeurs d'un tableau

=average(valeur₁ : valeur_n)

Mise à la puissance

=power(a,b).
Met a à la puissance b => a^b.

Racine carrée

=sqrt(x). Donne x^1/2

Variance d'une population

=varp(valeur₁ : valeur_n).
Formule en 1/n pour un tableau complet d'exercice de math.

Écart type d'une population

=stdevp(valeur₁ : valeur_n).
Formule en 1/n pour un tableau complet.

Et aussi

Factoriel de n (n!)

=fact(n).

[Accueil du site. ] _ [Lycée] _ [GAFAM et commen y échapper.]

Page validée W3C